← All posts

Parsing / Context-Free Grammar/Leftmost and Rightmost Derivations

A derivation of a string for a grammar is a sequence of production rule applications.

The process of getting the string through the derivation is the parsing process.

For example, with the following grammar:

S → S + S        (1)
S → 1            (2)
S → a            (3)

The string $1+1+a$ can be derived from the start symbol $S$ using 2 types of derivations: leftmost derivation and rightmost derivation.

Leftmost Derivation

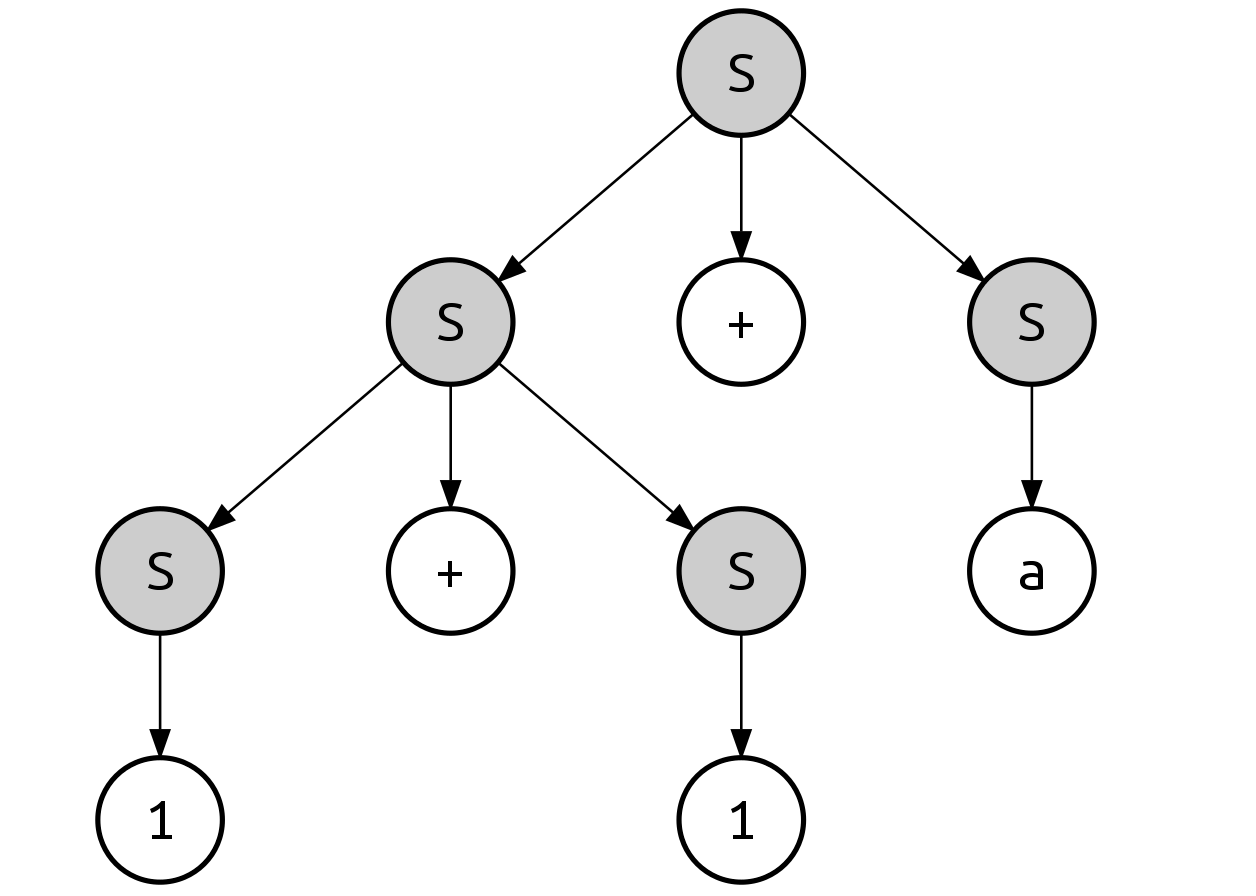
In the leftmost derivation, the nonterminals are applied from left to right. Initially, we can apply rule 1 on the initial $S$:

$$\to \underset{―}{S+S}\text{(applied rule 1)}$$

Next, the leftmost $S$ can be applied with rule 2:

$$\to \underset{―}{1}+S\text{(applied rule 2)}$$

The next nonterminal is the second $S$. If we apply any of rule 2 or 3, there are still underived characters in the input string, so we choose rule 1 instead:

$$\to 1+\underset{―}{S+S}\text{(applied rule 1)}$$

Now, with the remaining characters from the input, we can apply rule 2 on the first $S$:

$$\to 1+\underset{―}{1}+S\text{(applied rule 2)}$$

Finally, the last $S$ can be applied with rule 3:

$$\to 1+1+\underset{―}{a}\text{(applied rule 3)}$$

The above derivation can be represented as the following parse tree:

Rightmost Derivation

In the rightmost derivation, the nonterminals are applied from right to left.

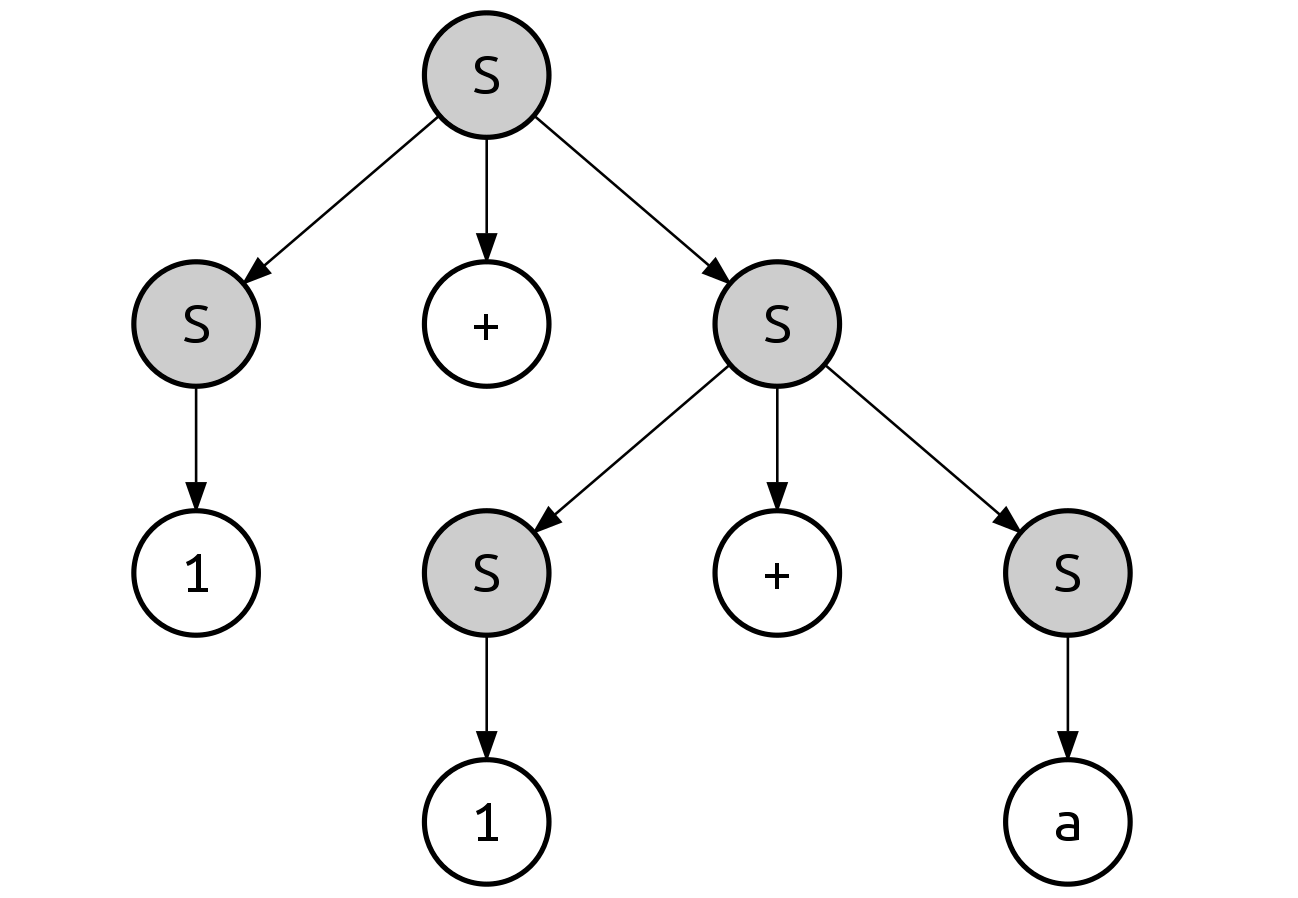
Initially, we can apply rule 1 on the initial $S$:

$$\to \underset{―}{S+S}\text{(applied rule 1)}$$

This time, we apply rule 1 on the rightmost $S$:

$$\to S+\underset{―}{S+S}\text{(applied rule 1)}$$

We found that rule 3 can be applied to the rightmost $S$:

$$\to S+S+\underset{―}{a}\text{(applied rule 3)}$$

Next, we can apply rule 2:

$$\to S+\underset{―}{1}+a\text{(applied rule 2)}$$

And finally, rule 2 can be applied again:

$$\to \underset{―}{1}+1+a\text{(applied rule 2)}$$

This derivation can be represented as the following parse tree:

---